A recent paper from Google DeepMind, "On the Theoretical Limitations of Embedding-Based Retrieval," provides a formal basis for a limitation many of us have intuited in single-vector retrieval systems. It's an important piece of work because it moves the discussion of embedding capacity onto a more rigorous, mathematical footing, forcing us to reconsider the ultimate capabilities of our simplest architectures.

The timing is also notable, as Google launched its new Gemma family of embedding models in the same week. It's ironic that Google's research organization publishing a fundamental critique of a technology while the product division ships a state-of-the-art implementation of it. 

This post will deconstruct the paper's technical argument, connect it to tangible engineering challenges, and explore the practical architectural implications for those of us building retrieval systems.

It's Not About Semantics, It's About Combinatorics

Before getting into the details, it's important to clarify what the paper proves. This isn't about a model's inability to understand language. It's about a d-dimensional vector's inability to geometrically partition a space of n documents in (n choose k) different ways.

The paper formalizes the problem as a low-rank matrix factorization problem:

1. Your retrieval task is a binary relevance matrix A.
2. Your embedding model's output is a score matrix B = U^T V, where d is your embedding dimension.
3. The hard constraint is that rank(B) ≤ d.

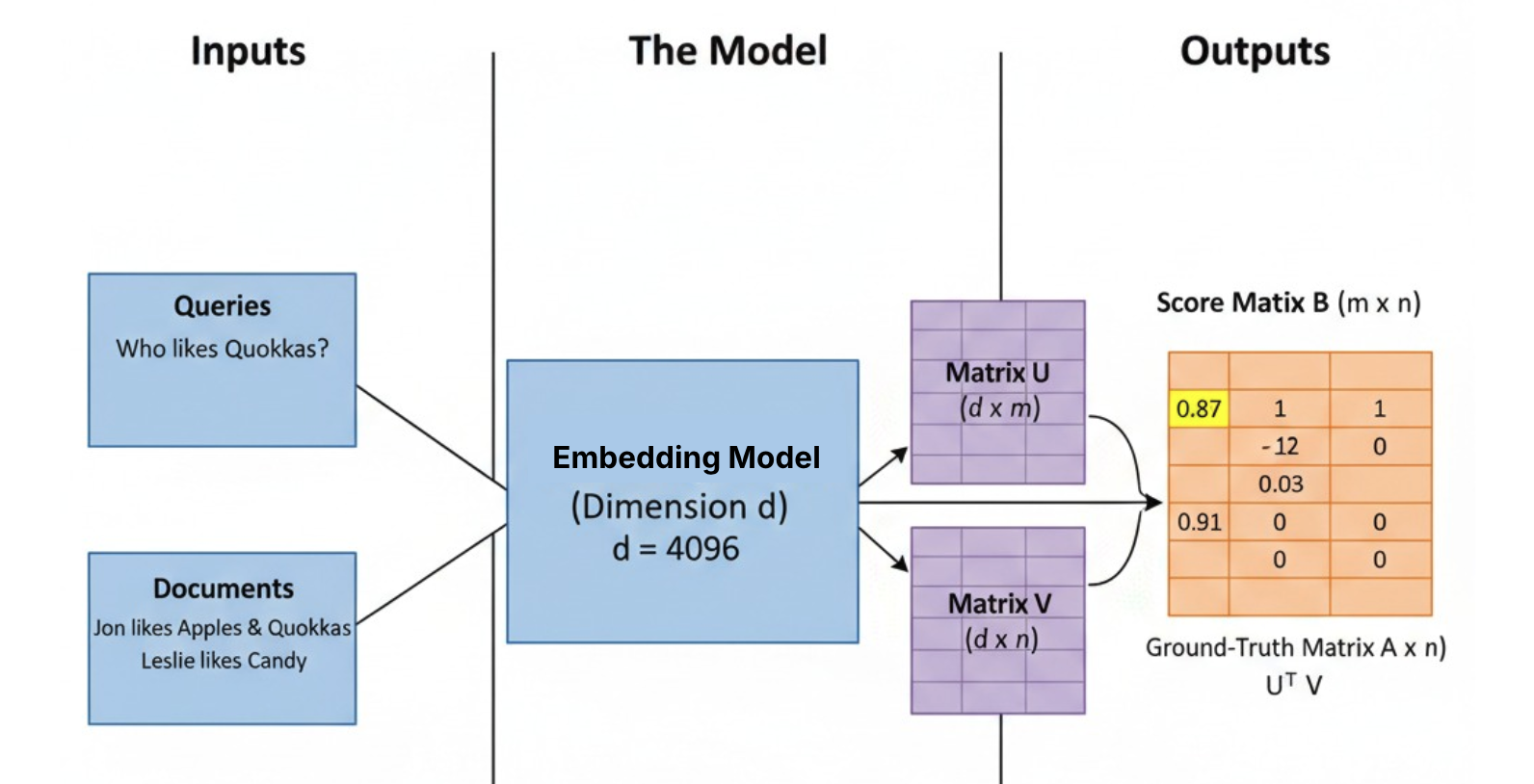
The authors then connect this to sign rank (rank_±), a well-studied concept from communication complexity. By transforming the {0, 1} relevance matrix A into a {-1, +1} matrix M = 2A - 1, they prove the following tight bound on the required dimension d:

rank_±(M) - 1 ≤ d_required ≤ rank_±(M)

This is the paper's core theoretical tool. It establishes the sign rank of the relevance matrix as a direct proxy for the "combinatorial complexity" of a retrieval task. The -1 in the lower bound isn't just mathematical slack; it comes directly from the proof, representing the rank-1 matrix of per-row thresholds (τ1^T) needed to map a retrieval solution to a sign-rank solution.

Empirical Validation: Finding the "Critical-n Point"

To test this theory, the authors design an idealized "free embedding optimization." They dispense with a language model and directly optimize n document vectors to be able to retrieve all possible k=2 combinations. This (n choose 2) task is a maximal stress test of the space's combinatorial capacity.

They incrementally increase n for a fixed dimension d until the optimizer fails to achieve 100% accuracy, finding the "critical-n point."

A valid critique has been raised about the reliability of extrapolating the resulting polynomial fit by two orders of magnitude. While the exact critical-n values should be taken with a grain of salt, the core finding—that the relationship is polynomial and not exponential—is the key insight. Even if the extrapolation is off by 50%, the conclusion remains the same: the capacity limit is real and well within the bounds of real-world corpus sizes.

Notable examples of the vector bottlenecks we’re hitting today:

• A d=512 model (e.g., some smaller BERTs): The breaking point is around n = 500k documents. Beyond this, it's guaranteed to fail on some top-2 combinations.
• A d=1024 model (common size): Breaks at n = 4 million documents.
• A massive d=4096 model (largest current models): Breaks at n = 250 million documents.

LIMIT: A Diagnostic for Production Pain Points

The paper's most potent contribution is the LIMIT dataset. It's engineered to have a high sign rank by instantiating a dense relevance graph: its core is a set of 1035 queries designed to retrieve every possible pair from a pool of 46 documents.

While few real-world datasets have this exact adversarial structure, the types of queries it simulates are becoming increasingly common. Many teams have encountered the downstream effects of this limitation in production:

• In RAG Systems: Consider the query, "Compare the fiscal policies of FDR and Reagan." A single-vector model is incentivized to find a single, shallow document that mentions both. What the user actually wants are the two best documents—one on New Deal economics and one on Reaganomics—fed into the context window simultaneously. This is a combinatorial retrieval task that single-vector search is notoriously bad at. It averages out user intent instead of satisfying its distinct components.
• In E-commerce Search: Anyone who has built a product search engine has felt this. A query for "blue trail-running shoes, size 10, under $100" gets compressed into a single point in space. The results are often a frustrating mix of shoes that are blue or size 10 or for trails, because the vector lacks the dimensions to precisely satisfy all orthogonal constraints at once.

The results on LIMIT are telling. State-of-the-art single-vector models perform poorly, with most achieving <20% recall@100. This failure is not due to domain shift; it's architectural. In contrast, ColBERT (multi-vector) and BM25 (high-dimensional sparse) perform substantially better. The problem isn't the task; it's the tool.

Conclusion: Hybrid Search and Reranking aren't crutches

This paper does not signal the end of dense retrieval. It signals the end of its misapplication as a universal solution. The single-vector embedding is a powerful tool, but it is a lossy one, and we now have a formal understanding of what is lost: combinatorial precision.

So, what should we do now?

1. Stop blindly scaling d. The poor returns on increasing embedding dimensions to solve a combinatorial problem should now be obvious. The cost in storage, memory, and latency for a marginal gain in capacity is a bad trade.
2. Start architecting for compositionality. For too long, we've treated hybrid search as a fallback—a messy concession that dense search isn't perfect. This paper reframes it. Hybrid search isn't a crutch; it's the correct architecture.

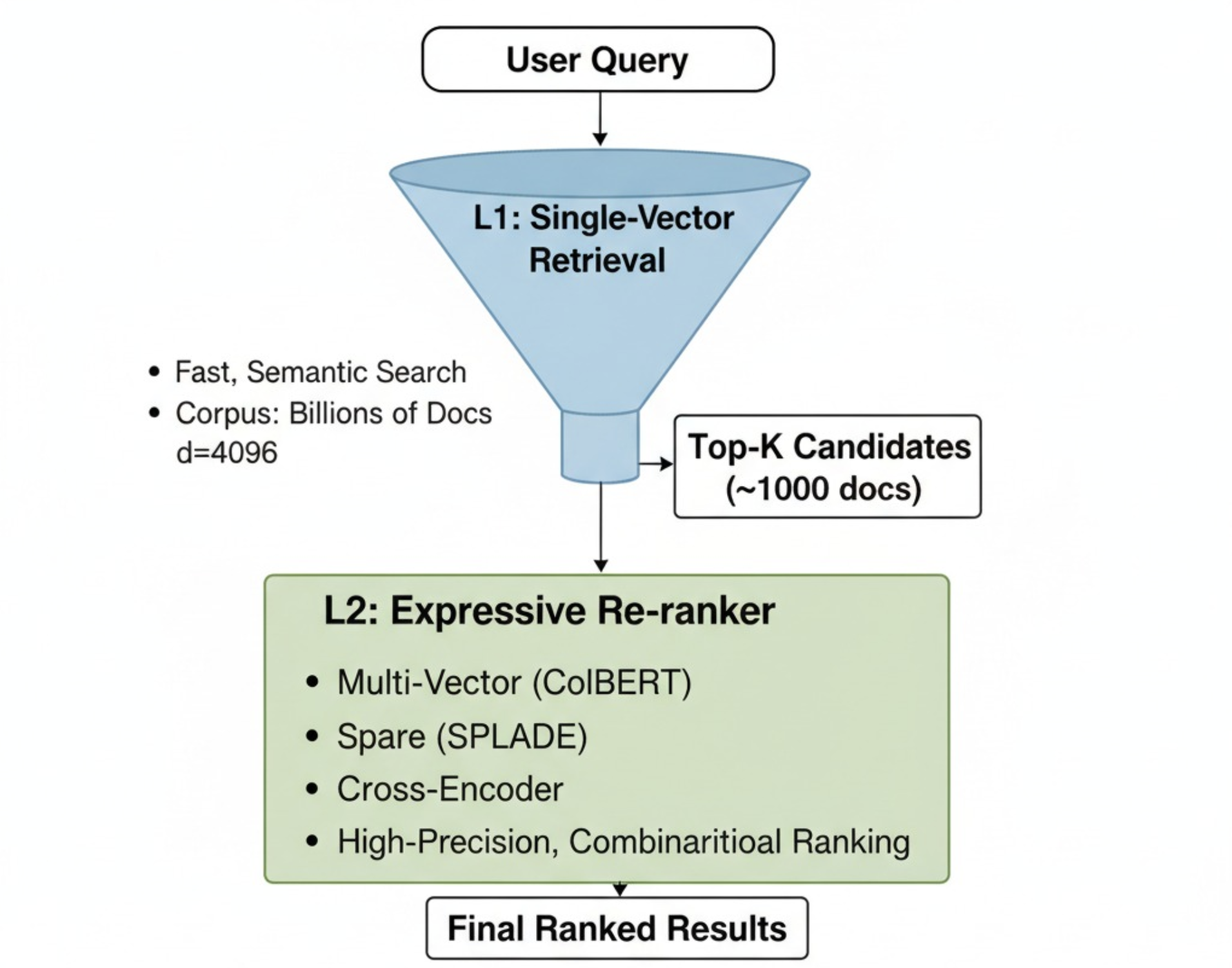
Here’s a prescriptive way to think about it: The single-vector embedding is your system's blazing-fast L1 cache for semantics. Its job is to solve the recall problem at scale, narrowing a massive corpus down to a few thousand candidates.

But a CPU isn't just a cache; it has an ALU for logic. Similarly, your retrieval system needs a higher-rank L2 component to execute the precise combinatorial logic that a single vector cannot. This means integrating architectures designed for expressiveness:

• Multi-vector models (ColBERT) for richer dense re-ranking.
• Sparse models (SPLADE) to leverage high-dimensional lexical and semantic signals.
• Cross-encoders when accuracy is non-negotiable.

Here’s a simple heuristic: if your users' queries are compositional, your retrieval system must be too. If you're combining filters, asking for comparisons, or need to retrieve distinct pieces of evidence, you are operating in a high-sign-rank world. A single vector will eventually, and inevitably, fail you. It's time to start building systems that acknowledge this reality.